Judul: Asal mula e
Ditulis oleh: Nabih pada Juni 15, 2009, 12:08:14 PM
Ditulis oleh: Nabih pada Juni 15, 2009, 12:08:14 PM
belajar kalkulus, kok banyak nager huruf, e
pertanyaan
1. dari mana tuh?
2, apa yang menyebabkan e begitu istimewa?
pertanyaan
1. dari mana tuh?
2, apa yang menyebabkan e begitu istimewa?
Judul: Re: Asal mula e
Ditulis oleh: HyawehHoshikawa pada Juni 15, 2009, 08:07:30 PM
Ditulis oleh: HyawehHoshikawa pada Juni 15, 2009, 08:07:30 PM
e itu kan basisnya logaritma natural...untuk ngitung luas kurva dibawah grafik y=x-1,
kalo' ga salah mas Kerajaan MTK bilang:
^n)
kalo' ga salah mas Kerajaan MTK bilang:
Judul: Re: Asal mula e
Ditulis oleh: Nabih pada Juni 15, 2009, 08:29:24 PM
Ditulis oleh: Nabih pada Juni 15, 2009, 08:29:24 PM
Maksih buat Hoshikawa
IQ+1 buat Hoshikawa
asal mulanya dari mana yaa
IQ+1 buat Hoshikawa
asal mulanya dari mana yaa
Judul: Re: Asal mula e
Ditulis oleh: Sky pada Juni 15, 2009, 11:00:42 PM
Ditulis oleh: Sky pada Juni 15, 2009, 11:00:42 PM
e adalah bilangan yang sangat istimewa, bro.
Seperti yang hoshikawa bilang, awalnya matematikawan berusaha mencari luas daerah di bawah kurva y=1/x
Kemudian, didapatlah fungsi itu, (misalnya f(x)) yang merupakan integral dari fungsi y(x) tadi.
Tepatnya:
=\int_0^x \frac 1x dx)
Setelah diteliti lebih lanjut, ternyata si f(x) ini adalah suatu fungsi logaritma.
Kan matematikawan jadi penasaran tuh? Jika f(x) adalah fungsi logaritma, maka pasti ada basisnya, dicarilah basisnya yang ternyata adalah suatu bilangan irrasional (sebut saja a) yang besarnya sekitar 2,178.
Karena matematikawan memang suka penasaran, sekarang mereka membuat fungsi invers dari f(x).
Sebut saja fungsi invers ini adalah g(x).=f^{-1}(x))
Karena f(x) adalah fungsi logaritma, maka fungsi inversnya adalah fungsi eksponen dengan basis a tadi.
Kalau kita tulis:=f^{-1}(x)=a^x)
Tapi, matematikawan tersebut melihat suatu keunikan, yaitu fungsi eksponen tersebut (g(x)) ternyata jika diturunkan adalah fungsi itu sendiri.....
Kalau ditulis:
Dan yang lebih mengejutkan lagi, ternyata banyak peristiwa di alam yang mengikuti persamaan differensial ini.
Contoh mudahnya: peluruhan radioaktif, laju peluruhannya (turunan dari peluruhan) sebanding dengan peluruhan itu sendiri.
Karena alasan keunikan, maka f(x) diberi nama "logaritma natural" (logaritma alamiah) yang diberi nama singkat=ln(x)) . Sedangkan basisnya, (a yang tadi) diberi nama basis natural, dan diberi simbol
. Sedangkan basisnya, (a yang tadi) diberi nama basis natural, dan diberi simbol 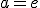 .
.
Kenapa ? Kenapa tidak a, b, atau c, atau d?
? Kenapa tidak a, b, atau c, atau d?
Karena ini untuk menghormati matematikawan yang mengusulkan pengunikan itu, yaitu seorang matematikawan yang bernama Euler. sehingga ini juga sering disebut bilangan Euler atau konstanta Euler.
ini juga sering disebut bilangan Euler atau konstanta Euler.
Seperti yang hoshikawa bilang, awalnya matematikawan berusaha mencari luas daerah di bawah kurva y=1/x
Kemudian, didapatlah fungsi itu, (misalnya f(x)) yang merupakan integral dari fungsi y(x) tadi.
Tepatnya:
Setelah diteliti lebih lanjut, ternyata si f(x) ini adalah suatu fungsi logaritma.
Kan matematikawan jadi penasaran tuh? Jika f(x) adalah fungsi logaritma, maka pasti ada basisnya, dicarilah basisnya yang ternyata adalah suatu bilangan irrasional (sebut saja a) yang besarnya sekitar 2,178.
Karena matematikawan memang suka penasaran, sekarang mereka membuat fungsi invers dari f(x).
Sebut saja fungsi invers ini adalah g(x).
Karena f(x) adalah fungsi logaritma, maka fungsi inversnya adalah fungsi eksponen dengan basis a tadi.
Kalau kita tulis:
Tapi, matematikawan tersebut melihat suatu keunikan, yaitu fungsi eksponen tersebut (g(x)) ternyata jika diturunkan adalah fungsi itu sendiri.....
Kalau ditulis:
Dan yang lebih mengejutkan lagi, ternyata banyak peristiwa di alam yang mengikuti persamaan differensial ini.
Contoh mudahnya: peluruhan radioaktif, laju peluruhannya (turunan dari peluruhan) sebanding dengan peluruhan itu sendiri.
Karena alasan keunikan, maka f(x) diberi nama "logaritma natural" (logaritma alamiah) yang diberi nama singkat
Kenapa
Karena ini untuk menghormati matematikawan yang mengusulkan pengunikan itu, yaitu seorang matematikawan yang bernama Euler. sehingga
Judul: Re: Asal mula e
Ditulis oleh: Mtk Kerajaan Mataram pada Juni 16, 2009, 06:41:23 AM
Ditulis oleh: Mtk Kerajaan Mataram pada Juni 16, 2009, 06:41:23 AM
I just realized that "Sky" was math educated. Excelent explanation.... thank you.
Judul: Re: Asal mula e
Ditulis oleh: Sky pada Juni 16, 2009, 06:48:11 AM
Ditulis oleh: Sky pada Juni 16, 2009, 06:48:11 AM
waduh....
thx bgt om Mataram...
Jd tersipu2 nih.....
thx bgt om Mataram...
Jd tersipu2 nih.....
Judul: Re: Asal mula e
Ditulis oleh: HyawehHoshikawa pada Juni 16, 2009, 12:39:34 PM
Ditulis oleh: HyawehHoshikawa pada Juni 16, 2009, 12:39:34 PM
@sky
)
 loh kok bukan 1 ???
loh kok bukan 1 ???
begitu toh ceritanya, pantesan dulu pas praktikum peluruhan malah pake' air seperti ini pada tabung fluida bocor itu yang berlaku:

padahal pada fluida tersebut

sehingga



dengan C = ketinggian awal...
ada yang bisa nglanjut ga supaya ketauan berapa "t"-nya supaya h=C
hehe sori OOT :P
enw, masih ada yang bikin penasaran ni, darimana yah ketemu persamaan:
^n)
KutipDan yang lebih mengejutkan lagi, ternyata banyak peristiwa di alam yang mengikuti persamaan differensial ini.hoo...
Contoh mudahnya: peluruhan radioaktif, laju peluruhannya (turunan dari peluruhan) sebanding dengan peluruhan itu sendiri.
begitu toh ceritanya, pantesan dulu pas praktikum peluruhan malah pake' air seperti ini pada tabung fluida bocor itu yang berlaku:
padahal pada fluida tersebut
sehingga
dengan C = ketinggian awal...
ada yang bisa nglanjut ga supaya ketauan berapa "t"-nya supaya h=C
hehe sori OOT :P
enw, masih ada yang bikin penasaran ni, darimana yah ketemu persamaan:
Judul: Re: Asal mula e
Ditulis oleh: Nabih pada Juni 16, 2009, 05:00:04 PM
Ditulis oleh: Nabih pada Juni 16, 2009, 05:00:04 PM
@ Sky
+1 IQ ah, makasih lho
@Hoshikawa
-h+C = \int \sqrt{2gh} dt
h=C berarti \int \sqrt{2gh} dt = 0
\sqrt{2gh} = 0
masak h=0, maksa banget, hahahahaha
+1 IQ ah, makasih lho
@Hoshikawa
-h+C = \int \sqrt{2gh} dt
h=C berarti \int \sqrt{2gh} dt = 0
\sqrt{2gh} = 0
masak h=0, maksa banget, hahahahaha
Judul: Re: Asal mula e
Ditulis oleh: Sky pada Juni 16, 2009, 07:21:12 PM
Ditulis oleh: Sky pada Juni 16, 2009, 07:21:12 PM
laju peluruhan sebanding dengan peluruhan itu maksudnya gini...
Misalkan peluruhan itu kita beri variabel N, jadinya:
 (karena kesebandingan, supaya jadi persamaan maka dikalikan konstanta)
(karena kesebandingan, supaya jadi persamaan maka dikalikan konstanta)
 (variabel yang sama harus dikelompokkan, yaitu N)
(variabel yang sama harus dikelompokkan, yaitu N)
 (kedua ruas diintegralkan)
(kedua ruas diintegralkan)
=kt+C) (penyataan ini ekuivalen dengan:)
(penyataan ini ekuivalen dengan:)

 (
( untuk memudahkan penulisan)
untuk memudahkan penulisan)
 (rumus peluruhan)
(rumus peluruhan)
@Hoshikawa
@nabih
Wow...tank-Q, mas nabih...
Misalkan peluruhan itu kita beri variabel N, jadinya:
@Hoshikawa
Kutip dari: HyawehHoshikawa pada Juni 16, 2009, 12:39:34 PMSampai sini sudah benar, tapi kalau mau diselesaikan, variabel yang sama harus dikelompokkan (h).
padahal pada fluida tersebut
sehingga
@nabih
Wow...tank-Q, mas nabih...
Judul: Re: Asal mula e
Ditulis oleh: HyawehHoshikawa pada Juni 16, 2009, 10:08:41 PM
Ditulis oleh: HyawehHoshikawa pada Juni 16, 2009, 10:08:41 PM
hoo...
kalo' gitu gimana kalo'




jadi mungkin supaya ketemu waktu pas h=C mungkin tinggal diganti aja yah?berarti itu bukan fungsi exponensial yah???
kalo' gitu gimana kalo'
jadi mungkin supaya ketemu waktu pas h=C mungkin tinggal diganti aja yah?berarti itu bukan fungsi exponensial yah???
Judul: Re: Asal mula e
Ditulis oleh: nash pada Juni 16, 2009, 10:24:24 PM
Ditulis oleh: nash pada Juni 16, 2009, 10:24:24 PM
mav kalo agak lo-la,
kan f(x) adalah integral tentu dari 1/x,
lalu knapa f(x) bisa dsbut sbg fungsi logaritma?
mohon pnjelasannya
kan f(x) adalah integral tentu dari 1/x,
lalu knapa f(x) bisa dsbut sbg fungsi logaritma?
mohon pnjelasannya
Judul: Re: Asal mula e
Ditulis oleh: HyawehHoshikawa pada Juli 09, 2009, 08:38:23 PM
Ditulis oleh: HyawehHoshikawa pada Juli 09, 2009, 08:38:23 PM
om,

)
tapi kalo' misalnya a&b < 0 gimana?(walopun kalo' diliat dari luas daerahnya cuman tinggal dikasi tanda minus "-")
kan log untuk bilangan negatif ga' ada?
tapi kalo' misalnya a&b < 0 gimana?(walopun kalo' diliat dari luas daerahnya cuman tinggal dikasi tanda minus "-")
kan log untuk bilangan negatif ga' ada?
Judul: Re: Asal mula e
Ditulis oleh: Sky pada Juli 10, 2009, 01:30:16 PM
Ditulis oleh: Sky pada Juli 10, 2009, 01:30:16 PM
Waduh, sori... aku udah lama ga ol lama...
Kita coba jawab satu-satu ya...
tadinya saya definisikan :=\int^x_0 \frac 1xdx)
Seharusnya yang benar itu :=\int^x_1 \frac 1xdx)
Matematikawan kemudian mencoba meneliti sifat fungsi ini.
Kita coba bahas secara bertahap.
# Sifat 1:=0)
* Kita tahu bahwa jika=\int^x_1 \frac 1xdx) maka
maka +C)
Ini adalah prinsip integral tentu dan tak tentu.
* Kita gunakan kedua sifat tadi.
Kita hitung .
.
Karena+C) , maka
, maka ![\int^x_1 \frac 1xdx=\left[f(x)+C\right]^x_1](https://www.forumsains.com/cgi-bin/mimetex.cgi?\int^x_1 \frac 1xdx=\left[f(x)+C\right]^x_1)
Selesaikan ruas kiri:![f(x)=\left[f(x)+C\right]^x_1](https://www.forumsains.com/cgi-bin/mimetex.cgi?f(x)=\left[f(x)+C\right]^x_1)
Selesaikan ruas kanan :![f(x)=[f(x)+C]-[f(1)+C]](https://www.forumsains.com/cgi-bin/mimetex.cgi?f(x)=[f(x)+C]-[f(1)+C])
Maka didapat:=0)
Kita coba jawab satu-satu ya...
Kutip dari: HyawehHoshikawa pada Juni 16, 2009, 10:08:41 PMIya, kalo yang ini bukan fungsi eksponensial.
jadi mungkin supaya ketemu waktu pas h=C mungkin tinggal diganti aja yah?berarti itu bukan fungsi exponensial yah???
Kutip dari: nash pada Juni 16, 2009, 10:24:24 PMSebelumnya mau saya ralat dulu, karena baru sadar.
mav kalo agak lo-la,
kan f(x) adalah integral tentu dari 1/x,
lalu knapa f(x) bisa dsbut sbg fungsi logaritma?
mohon pnjelasannya
tadinya saya definisikan :
Seharusnya yang benar itu :
Sorry but you are not allowed to view spoiler contents.
Matematikawan kemudian mencoba meneliti sifat fungsi ini.
Kita coba bahas secara bertahap.
# Sifat 1:
* Kita tahu bahwa jika
Ini adalah prinsip integral tentu dan tak tentu.
* Kita gunakan kedua sifat tadi.
Kita hitung
Karena
Selesaikan ruas kiri:
Sorry but you are not allowed to view spoiler contents.
Selesaikan ruas kanan :
Maka didapat:
Sorry but you are not allowed to view spoiler contents.
Judul: Re: Asal mula e
Ditulis oleh: Sky pada Juli 10, 2009, 01:45:19 PM
Ditulis oleh: Sky pada Juli 10, 2009, 01:45:19 PM
# Sifat 2 : =f(a)+f(b))
* Dengan sedikit kreativitas, kita bisa buktikan bahwa
* Coba kita integralkan persamaan tadi.

 + C1=f(ax) +C2)
Kemudian, jika kita cari konstantanya dengan menyulihkan x=1, didapat:
 +C1=f(a)+C2)
)
Kemudian. kita sulihkan C1 dan C2:
+C1-C2=f(ax))
+f(a)=f(ax))
Jika x kita ganti suatu bilangan b, didapat:
+f(a)=f(ab))
* Dengan sedikit kreativitas, kita bisa buktikan bahwa
* Coba kita integralkan persamaan tadi.
Kemudian, jika kita cari konstantanya dengan menyulihkan x=1, didapat:
Kemudian. kita sulihkan C1 dan C2:
Jika x kita ganti suatu bilangan b, didapat:
Judul: Re: Asal mula e
Ditulis oleh: Sky pada Juli 10, 2009, 01:51:41 PM
Ditulis oleh: Sky pada Juli 10, 2009, 01:51:41 PM
Nah, kedua sifat tadi adalah identitas dasar fungsi logaritma.
Dari keduanya, bisa diturunkan sifat2 logaritma yang lain.
Seperti :
# Sifat 3:=-f(\frac 1a))
# Sifat 4:=f(a)-f(b))
Oya, penomoran sifat ini ga wajib.
Saya nomori begitu untuk memudahkan pembacaan dan notasi saja.
Nah, karena fungsi f(x) adalah fungsi logaritma, berarti fungsi ini memiliki basis tertentu, yang kemudian basis tersebut diberi nama bilangan e.
Dari keduanya, bisa diturunkan sifat2 logaritma yang lain.
Seperti :
# Sifat 3:
# Sifat 4:
Oya, penomoran sifat ini ga wajib.
Saya nomori begitu untuk memudahkan pembacaan dan notasi saja.
Nah, karena fungsi f(x) adalah fungsi logaritma, berarti fungsi ini memiliki basis tertentu, yang kemudian basis tersebut diberi nama bilangan e.
Judul: Re: Asal mula e
Ditulis oleh: Sky pada Juli 10, 2009, 02:30:58 PM
Ditulis oleh: Sky pada Juli 10, 2009, 02:30:58 PM
Kutip dari: HyawehHoshikawa pada Juli 09, 2009, 08:38:23 PMUntuk menjawab pertanyaan Hoshikawa kita harus meninjau dulu perilaku f(x) saat x<0.
om,
tapi kalo' misalnya a&b < 0 gimana?(walopun kalo' diliat dari luas daerahnya cuman tinggal dikasi tanda minus "-")
kan log untuk bilangan negatif ga' ada?
Karena, saat membahas sifat2 tadi, kita hanya menggunakan x>0.
* Kita hitung lagi dari awal: untuk x<0
Sorry but you are not allowed to view spoiler contents.
Nah, ternyata
Padahal, fungsi logaritma tidak terdefinisi di x<0, kan?
Sementara
Jadi kesimpulannya
Untuk menyatakan
Nah, tadi kan definisi awalnya
Sekarang, karena definisinya diperluas menjadi
Maka definisi integral tak tentunya juga mesti diubah, menjadi:
Perlu diingat, bahwa fungsi logaritmanya saja hanya terdefinisi untuk x>0.
Tapi f(x) terdefinisi juga untuk x<0 karena dia merupakan fungsi modifikasi dari fungsi logaritma.
Judul: Re: Asal mula e
Ditulis oleh: HyawehHoshikawa pada Juli 10, 2009, 04:00:23 PM
Ditulis oleh: HyawehHoshikawa pada Juli 10, 2009, 04:00:23 PM
eh, integralnya ln(x) itu kan x*ln(x) - x
terus kalo' integralnya:
) itu apa yah?
itu apa yah?
kok' gw coba di calc101 ama wolfram ga bisa?
integralnya xx juga ga ada...tapi turunannya ada.
terus kalo' integralnya:
kok' gw coba di calc101 ama wolfram ga bisa?
integralnya xx juga ga ada...tapi turunannya ada.
Judul: Re: Asal mula e
Ditulis oleh: sith lord pada Juli 18, 2009, 04:11:22 AM
Ditulis oleh: sith lord pada Juli 18, 2009, 04:11:22 AM
top markotop
Judul: Re: Asal mula e
Ditulis oleh: Zanra_GTG pada Agustus 18, 2009, 12:10:41 AM
Ditulis oleh: Zanra_GTG pada Agustus 18, 2009, 12:10:41 AM
klo ditanya darimana yach, dari sononya, tapi yg jelas e biasax digunakan pada logaritma natural(ln) e log x = n, maka e^n = x
jadi e log x = ln x
jadi e log x = ln x
Judul: Re: Asal mula e
Ditulis oleh: Mtk Kerajaan Mataram pada September 22, 2009, 12:14:18 AM
Ditulis oleh: Mtk Kerajaan Mataram pada September 22, 2009, 12:14:18 AM
Pertama kali bilangan e muncul hampir dianggap tidak penting. Pada tahun 1618, dalam apendik karya Napier tentang logaritma, sebuah tabel nampak memberikan logaritma natural terhadap barbagai macam bilangan. Namun, lagoritma berbasis e waktu itu belum dikenal karena bilangan e itu sendiri belum muncul seperti yang dikenal sekarang. Meskipun sekarang kita memandang logaritma sebagai pangkat yang akan dicari jika suatu bilangan basis dipangkatkan bil tsb menghasilkan suatu bilangan yang telah diketahui, namun ini adalah pemikiran modern sekarang ini. Beberapa tahun kemudian pada 1624, lagi-lagi bilangan e hampir dibawa ke literatur matematika, tapi tidak cukup. Pada saat itu, Briggs memberikan pendekatan numerik terhadap logaritma berbasis 10 terhadap e, tapi tidak menyebut e itu sendiri dalam karyanya.
Kemungkinan munculnya bilangan e waktu itu menjadi rancu lagi.Pada tahun 1647 Saint Vincent menghitung luas suatu hiperbola tegaklurus (kedua asimtotnya saling tegak lurus). Yang menjadi perdebatan adalah apakah dia mengenal hubungan antara luas tersebut dengan logaritma atau tidak, dan bahkan jika dia mengenalnya maka itu hanya merupakan alasan kecil baginya untuk membawa pada bilangan e secara eksplisit. Pastinya, pada tahun 1661 Huygen mengerti hubungan antara hiperbola tegaklurus dengan logaritma tsb. Dia menelaah secara eksplisit hubungan antara luas dibawah hiperbola tegaklurus xy=1 dan logaritma tsb. Yaitu bahwa luas dibawah kurva xy=1 dari 1 s.d. e sama dengan 1. Hal ini yang merupakan bahan untuk membuat e sebagai basis logaritma narural, namun waktu itu masih belum dimengerti oleh para matematikawan, meskipun pelan-pelan mereka mengarah kepada pemahaman ini.
Huygens melanjutkan dengan dengan cara lain pada tahun 1661. Dia mendefinisikan sebuah kurva yang dia sebut dengan logaritmik tapi kita lebih mengenalnya sebagai kurva eksponensial, yang berbentuk . Lagi dari sini diperoleh nilai logaritma dari e berbasis 10, yang oleh Huygens dihitung sampai 17 belakang koma, hasil ini muncul sebagai penghitungan dari suatu konstanta dari hasil kerjanya dan tidak dikenal sebagai logaritma suatu bilangan (Lagi-lagi merupakan kedekatan pada e, namun masih belum dikenal).
. Lagi dari sini diperoleh nilai logaritma dari e berbasis 10, yang oleh Huygens dihitung sampai 17 belakang koma, hasil ini muncul sebagai penghitungan dari suatu konstanta dari hasil kerjanya dan tidak dikenal sebagai logaritma suatu bilangan (Lagi-lagi merupakan kedekatan pada e, namun masih belum dikenal).
........................................
Selanjutnya dapat dibaca di [pranala luar disembunyikan, sila masuk atau daftar.].
Kemungkinan munculnya bilangan e waktu itu menjadi rancu lagi.Pada tahun 1647 Saint Vincent menghitung luas suatu hiperbola tegaklurus (kedua asimtotnya saling tegak lurus). Yang menjadi perdebatan adalah apakah dia mengenal hubungan antara luas tersebut dengan logaritma atau tidak, dan bahkan jika dia mengenalnya maka itu hanya merupakan alasan kecil baginya untuk membawa pada bilangan e secara eksplisit. Pastinya, pada tahun 1661 Huygen mengerti hubungan antara hiperbola tegaklurus dengan logaritma tsb. Dia menelaah secara eksplisit hubungan antara luas dibawah hiperbola tegaklurus xy=1 dan logaritma tsb. Yaitu bahwa luas dibawah kurva xy=1 dari 1 s.d. e sama dengan 1. Hal ini yang merupakan bahan untuk membuat e sebagai basis logaritma narural, namun waktu itu masih belum dimengerti oleh para matematikawan, meskipun pelan-pelan mereka mengarah kepada pemahaman ini.
Huygens melanjutkan dengan dengan cara lain pada tahun 1661. Dia mendefinisikan sebuah kurva yang dia sebut dengan logaritmik tapi kita lebih mengenalnya sebagai kurva eksponensial, yang berbentuk
........................................
Selanjutnya dapat dibaca di [pranala luar disembunyikan, sila masuk atau daftar.].
Judul: Re: Asal mula e
Ditulis oleh: Nabih pada November 11, 2009, 09:04:26 PM
Ditulis oleh: Nabih pada November 11, 2009, 09:04:26 PM
Kutip dari: HyawehHoshikawa pada Juli 10, 2009, 04:00:23 PMintegralitu apa yah?
=integral
=ln(a) integral
hayo berapa????
Judul: Re: Asal mula e
Ditulis oleh: The Houw Liong pada November 12, 2009, 06:53:15 AM
Ditulis oleh: The Houw Liong pada November 12, 2009, 06:53:15 AM