Judul: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Yorknell pada Agustus 11, 2010, 12:02:55 AM
Ditulis oleh: Yorknell pada Agustus 11, 2010, 12:02:55 AM
Salam warga forum sains, perkenalkan saya warga baru di sini :kribo: ;D.
Mau tanya nih, kan byk ni soal2 yang menyangkutpautkan dan berhubungan dengan akar pangkat dua dari bilangan non-kuadrat seperti akar 2, akar 5, dan seterusnya.
Saya pernah baca ada trik cepat menghitung akar kuadrat dari bilangan non-kuadrat yang sangat jitu dan cepat, dan melibatkan seperti penjumlahan dan angka ganjil (CMIIW).. Memang sih nda bisa sampai akurat 100% paling tidak bisa sampai berberapa angka di belakang koma lah (satu atau 2 yah?) misalnya akar akar 27 kan 3 akar 3 tuh.. nah itu bisa dijadikan koma ama dia.. gimana itu yah?? tolong donk trik cepatnya thx!
Mau tanya nih, kan byk ni soal2 yang menyangkutpautkan dan berhubungan dengan akar pangkat dua dari bilangan non-kuadrat seperti akar 2, akar 5, dan seterusnya.
Saya pernah baca ada trik cepat menghitung akar kuadrat dari bilangan non-kuadrat yang sangat jitu dan cepat, dan melibatkan seperti penjumlahan dan angka ganjil (CMIIW).. Memang sih nda bisa sampai akurat 100% paling tidak bisa sampai berberapa angka di belakang koma lah (satu atau 2 yah?) misalnya akar akar 27 kan 3 akar 3 tuh.. nah itu bisa dijadikan koma ama dia.. gimana itu yah?? tolong donk trik cepatnya thx!
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Fhydha_099 pada Agustus 11, 2010, 05:43:18 AM
Ditulis oleh: Fhydha_099 pada Agustus 11, 2010, 05:43:18 AM
Ohh, saya ngerti.
Maksudnya ∛27 = 3, sekian gitu??
Hmm.... Wah, pengetahuan saya belum sampai ke situ. Coba tanya sama senior saya, Sisca dan Huriah. Siapa tahu mereka tahu.
Maksudnya ∛27 = 3, sekian gitu??
Hmm.... Wah, pengetahuan saya belum sampai ke situ. Coba tanya sama senior saya, Sisca dan Huriah. Siapa tahu mereka tahu.
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Yorknell pada Agustus 11, 2010, 11:55:19 AM
Ditulis oleh: Yorknell pada Agustus 11, 2010, 11:55:19 AM
yup2 mksdnya gt..
thx yah setidaknya dh cuba bantu
dulu kalau ndak salah inget pernah nemu sih emang nda akurat 100% gt..
cuman kalo ndak salah sampe pecahan atau koma koma (tp cuman dua angka ato satu di belakang koma)
thx deh...
Gimana ya cara kontak cc itu?
thx yah setidaknya dh cuba bantu
dulu kalau ndak salah inget pernah nemu sih emang nda akurat 100% gt..
cuman kalo ndak salah sampe pecahan atau koma koma (tp cuman dua angka ato satu di belakang koma)
thx deh...
Gimana ya cara kontak cc itu?
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Yorknell pada Agustus 11, 2010, 01:13:00 PM
Ditulis oleh: Yorknell pada Agustus 11, 2010, 01:13:00 PM
MAAF salah baca.. bukan, maksudnya seperti ini..
kan akar kuadrat dari 2,3,5,7 itu tidak dpt diketahui dengan mudah
nah, gimana yah caranya supaya bisa tau perkiraan angkanya dgn krg lbh tpt..
thx
kan akar kuadrat dari 2,3,5,7 itu tidak dpt diketahui dengan mudah
nah, gimana yah caranya supaya bisa tau perkiraan angkanya dgn krg lbh tpt..
thx
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Blue_Rain pada Agustus 11, 2010, 05:39:37 PM
Ditulis oleh: Blue_Rain pada Agustus 11, 2010, 05:39:37 PM
Saya ada usul nih...
daripada menghitung coba hafalkan tabel akar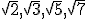
nah nanti kalo ada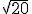
berarti kan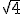 X
X 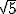
2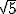
jadinya 2x2.23
hasil 4.46
tapi masalahnya itu baru akar 20 coba kalo akar 531 ngitungnya gimana ya...??
??? ??? ??? ??? ???
Any Idea?
daripada menghitung coba hafalkan tabel akar
nah nanti kalo ada
berarti kan
2
jadinya 2x2.23
hasil 4.46
tapi masalahnya itu baru akar 20 coba kalo akar 531 ngitungnya gimana ya...??
??? ??? ??? ??? ???
Any Idea?
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: david alberto christian pada Agustus 11, 2010, 06:20:19 PM
Ditulis oleh: david alberto christian pada Agustus 11, 2010, 06:20:19 PM
kayanya cara kakak blue rain itu bagus juga.. Hafalin aja tabel akar.. Emang sih rada susah kalo akar bilangan prima yang gede.. Tapi ada sih cara nyelesai-in akar irrasional tapi pake pendekatan, ga begitu akurat
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Yorknell pada Agustus 11, 2010, 08:45:01 PM
Ditulis oleh: Yorknell pada Agustus 11, 2010, 08:45:01 PM
yah itu dia hehehhe.. kalo akar 531 gmana ya heheh
btw ko david gimana tuh caranya.. boleh aja dicoba:D
btw ko david gimana tuh caranya.. boleh aja dicoba:D
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: The Houw Liong pada Agustus 12, 2010, 10:50:32 AM
Ditulis oleh: The Houw Liong pada Agustus 12, 2010, 10:50:32 AM
Kutip dari: Yorknell pada Agustus 11, 2010, 08:45:01 PM
yah itu dia hehehhe.. kalo akar 531 gmana ya heheh
btw ko david gimana tuh caranya.. boleh aja dicoba:D
Pakai rumus untuk x <<1 maka (1+x)^n = 1 + n.x + ...
(531)^0.5 = (576 -45)^0.5 = {576(1-45/576)}^0.5 = 24(1 - 0.5 *45/576) = 24 - 22,5/24 = 23,05
atau lebih tepat
(529+2)^0.5 = (529(1+2/529))^0.5 = 23(1+ 0.5*2/529) = 23 + 1/23 = 23,04
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: The Houw Liong pada Agustus 12, 2010, 11:55:21 AM
Ditulis oleh: The Houw Liong pada Agustus 12, 2010, 11:55:21 AM
Kutip dari: The Houw Liong pada Agustus 12, 2010, 10:50:32 AMKutip dari: Yorknell pada Agustus 11, 2010, 08:45:01 PM
yah itu dia hehehhe.. kalo akar 531 gmana ya heheh
btw ko david gimana tuh caranya.. boleh aja dicoba:D
Pakai rumus untuk x <<1 maka (1+x)^n = 1 + n.x + (n.(n+1)/2 ). x^2 + ...
(531)^0.5 = (576 -45)^0.5 = {576(1-45/576)}^0.5 = 24(1 - 0.5 *45/576) = 24 - 22,5/24 = 23,05
atau lebih tepat
(529+2)^0.5 = (529(1+2/529))^0.5 = 23(1+ 0.5*2/529) = 23 + 1/23 = 23,04
Sebaliknya :
(23,05)^2 = (23+ 0,5)^2 = (23 ( 1+ 0,5/23))^2 = 529 + 23/23 + (3/2) 0.5/23 + .. = 531
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Fachni Rosyadi pada Agustus 12, 2010, 01:11:45 PM
Ditulis oleh: Fachni Rosyadi pada Agustus 12, 2010, 01:11:45 PM
Kalau caraku gini.
Misal kita ingin mencari nilai dari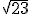 . Kita tahu bahwa
. Kita tahu bahwa 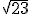 terletak antara
terletak antara 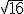 dan
dan 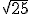 .
.
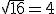

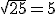
Jadi, .
.
Misal kita ingin mencari nilai dari
Jadi,
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: The Houw Liong pada Agustus 12, 2010, 01:35:22 PM
Ditulis oleh: The Houw Liong pada Agustus 12, 2010, 01:35:22 PM
Kutip dari: The Houw Liong pada Agustus 12, 2010, 11:55:21 AMKutip dari: The Houw Liong pada Agustus 12, 2010, 10:50:32 AMKutip dari: Yorknell pada Agustus 11, 2010, 08:45:01 PM
yah itu dia hehehhe.. kalo akar 531 gmana ya heheh
btw ko david gimana tuh caranya.. boleh aja dicoba:D
Pakai rumus untuk x <<1 maka (1+x)^n = 1 + n.x + (n.(n-1)/2 ). x^2 + ...
(531)^0.5 = (576 -45)^0.5 = {576(1-45/576)}^0.5 = 24(1 - 0.5 *45/576) = 24 - 22,5/24 = 23,05
atau lebih tepat
(529+2)^0.5 = (529(1+2/529))^0.5 = 23(1+ 0.5*2/529) = 23 + 1/23 = 23,04
Sebaliknya :
(23,05)^2 = (23+ 0,05)^2 = (23 ( 1+ 0,05/23))^2 = 529 + 2,3 + 23^2.(0,05/23)^2 = 531,3
Yang mendekati tepat ialah 23,045 ^ 2 = 531,072
Ada koreksi rumus.
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Fhydha_099 pada Agustus 12, 2010, 04:18:05 PM
Ditulis oleh: Fhydha_099 pada Agustus 12, 2010, 04:18:05 PM
Waduh ... :o :o
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: The Houw Liong pada Agustus 12, 2010, 04:51:27 PM
Ditulis oleh: The Houw Liong pada Agustus 12, 2010, 04:51:27 PM
Kutip dari: Fachni Rosyadi pada Agustus 12, 2010, 01:11:45 PM
Kalau caraku gini.
Misal kita ingin mencari nilai dari. Kita tahu bahwa
terletak antara
dan
.
Jadi,.
(23^0,5) = (25-2)^0,5 = (25^0,5)(1- 2/25)^0,5 = 5( 1- 0,5. 2/25) = 5 - 5/25 =
5 - 0,20 = 4,80
Cek :
4,80^2 = 23,04
4,78^2 = 22,84
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Bernando pada Agustus 13, 2010, 10:10:42 AM
Ditulis oleh: Bernando pada Agustus 13, 2010, 10:10:42 AM
coba aja pake rata2...
contoh :
kita mau cari akar 4..
misalkan hasilnya adalah x
akar 4 = x --> x^2 = 4
x . x = 4 --> x = 4 / x
artinya ketika hasil dari akar tersebut (4) dibagi dengan x hasilnya sama dengan x..
misal kita terka hasil yang mendekati nilai x...semakin dekat ke jawaban maka akan semakin cepat dapat hasilnya...
contoh kita kasih sembarang nilai untuk x = 1...
x = 4 / x kita subs nilai x = 1...
berarti 1 = 4 / 1 --> 1 = 4 ... kondisi ini kan masih salah
sekarang kita ganti nilai x dengan (1 + 4) / 2 --> 2,50
nah sekarang nilai x = 2,50
x = 4 / x --> 2,50 = 4 / 2,50 --> 2,50 = 1,60 --> x = 2,05
x = 4 / x --> 2,05 = 4 / 2,05 --> 2,05 = 1,95 --> x = 2
x = 4 / x --> 2 = 4 / 2 --> 2 = 2 --> kondisi sudah benar
berarti kesimpulannya akar 4 = 2
dengan cara yang sama coba aja dengan akar 5, akar 6, dst....:D
contoh :
kita mau cari akar 4..
misalkan hasilnya adalah x
akar 4 = x --> x^2 = 4
x . x = 4 --> x = 4 / x
artinya ketika hasil dari akar tersebut (4) dibagi dengan x hasilnya sama dengan x..
misal kita terka hasil yang mendekati nilai x...semakin dekat ke jawaban maka akan semakin cepat dapat hasilnya...
contoh kita kasih sembarang nilai untuk x = 1...
x = 4 / x kita subs nilai x = 1...
berarti 1 = 4 / 1 --> 1 = 4 ... kondisi ini kan masih salah
sekarang kita ganti nilai x dengan (1 + 4) / 2 --> 2,50
nah sekarang nilai x = 2,50
x = 4 / x --> 2,50 = 4 / 2,50 --> 2,50 = 1,60 --> x = 2,05
x = 4 / x --> 2,05 = 4 / 2,05 --> 2,05 = 1,95 --> x = 2
x = 4 / x --> 2 = 4 / 2 --> 2 = 2 --> kondisi sudah benar
berarti kesimpulannya akar 4 = 2
dengan cara yang sama coba aja dengan akar 5, akar 6, dst....:D
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Yorknell pada Agustus 13, 2010, 06:20:06 PM
Ditulis oleh: Yorknell pada Agustus 13, 2010, 06:20:06 PM
thx2 semuanya.. nti ak coba ya.. lg ol pake hp :p ni.. nti segera kucoba deh.. ada saran lain? thx
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Yorknell pada Agustus 15, 2010, 09:23:40 PM
Ditulis oleh: Yorknell pada Agustus 15, 2010, 09:23:40 PM
Kutip dari: The Houw Liong pada Agustus 12, 2010, 10:50:32 AMmaksudnya apa ya?? gw rada bingung hehehe thxKutip dari: Yorknell pada Agustus 11, 2010, 08:45:01 PM
yah itu dia hehehhe.. kalo akar 531 gmana ya heheh
btw ko david gimana tuh caranya.. boleh aja dicoba:D
Pakai rumus untuk x <<1 maka (1+x)^n = 1 + n.x + ...
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: The Houw Liong pada Agustus 16, 2010, 06:45:23 AM
Ditulis oleh: The Houw Liong pada Agustus 16, 2010, 06:45:23 AM
Kutip dari: Yorknell pada Agustus 15, 2010, 09:23:40 PMRumus itu adalah uraian deret misalnya akar 11 , caranya :Kutip dari: The Houw Liong pada Agustus 12, 2010, 10:50:32 AMmaksudnya apa ya?? gw rada bingung hehehe thxKutip dari: Yorknell pada Agustus 11, 2010, 08:45:01 PM
yah itu dia hehehhe.. kalo akar 531 gmana ya heheh
btw ko david gimana tuh caranya.. boleh aja dicoba:D
Pakai rumus untuk x <<1 maka (1+x)^n = 1 + n.x + ...
1. Cari bilangan kuadrat terdekat dengan 11, yaitu 9 = 3^2.
2. Tulis 11 = 9 + 2, akar 11 = akar ( 9+2) = akar 3^2 ( 1 + 2/9).
3. Gunakan uraian deret (1+2/9)^0,5 = 1 + 0,5(2/9)
4. Maka akar 11 = 3(1+ 1/9) = 3,333
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Blue_Rain pada Agustus 16, 2010, 05:26:13 PM
Ditulis oleh: Blue_Rain pada Agustus 16, 2010, 05:26:13 PM
Kutip dari: The Houw Liong pada Agustus 16, 2010, 06:45:23 AM
Rumus itu adalah uraian deret misalnya akar 11 , caranya :
1. Cari bilangan kuadrat terdekat dengan 11, yaitu 9 = 3^2.
2. Tulis 11 = 9 + 2, akar 11 = akar ( 9+2) = akar 3^2 ( 1 + 2/9).
3. Gunakan uraian deret (1+2/9)^0,5 = 1 + 0,5(2/9)
4. Maka akar 11 = 3(1+ 1/9) = 3,333
Saya sendiri juga masih rada bingung tapi saya coba untuk tulis dalam notasi matematikanya biar rada jelas sedikit...(mungkin)
1. Cari bilangan kuadrat terdekat dengan 11, yaitu 9 = 3².
2. Tulis 11 = 9 + 2,
(http://latex.codecogs.com/gif.download?%5Csqrt&space;%7B11%7D&space;=&space;%5Csqrt&space;%7B9+2%7D&space;=&space;%5Csqrt&space;%7B3%5E2(1+%5Cfrac%7B2%7D%7B9%7D)%7D)
3. Gunakan Uraian Deret
(http://latex.codecogs.com/gif.download?(1+%5Cfrac%7B2%7D%7B9%7D)%5E%7B0.5%7D=&space;1+0.5(%5Cfrac%7B2%7D%7B9%7D))
Nah, di poin yang ketiga ini yang saya kurang mengerti. Maksudnya uraian deret itu apa yah??
??? ???
4. Maka akar 11 = 3(1+ 1/9) = 3,333
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Nabih pada September 01, 2010, 09:14:23 AM
Ditulis oleh: Nabih pada September 01, 2010, 09:14:23 AM
Pake aja metode heron
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: The Houw Liong pada September 01, 2010, 10:04:04 AM
Ditulis oleh: The Houw Liong pada September 01, 2010, 10:04:04 AM
Kutip dari: Blue_Rain pada Agustus 16, 2010, 05:26:13 PMKutip dari: The Houw Liong pada Agustus 16, 2010, 06:45:23 AM
Rumus itu adalah uraian deret misalnya akar 11 , caranya :
1. Cari bilangan kuadrat terdekat dengan 11, yaitu 9 = 3^2.
2. Tulis 11 = 9 + 2, akar 11 = akar ( 9+2) = akar 3^2 ( 1 + 2/9).
3. Gunakan uraian deret (1+2/9)^0,5 = 1 + 0,5(2/9)
4. Maka akar 11 = 3(1+ 1/9) = 3,333
Saya sendiri juga masih rada bingung tapi saya coba untuk tulis dalam notasi matematikanya biar rada jelas sedikit...(mungkin)
1. Cari bilangan kuadrat terdekat dengan 11, yaitu 9 = 3².
2. Tulis 11 = 9 + 2,
(http://latex.codecogs.com/gif.download?%5Csqrt&space;%7B11%7D&space;=&space;%5Csqrt&space;%7B9+2%7D&space;=&space;%5Csqrt&space;%7B3%5E2(1+%5Cfrac%7B2%7D%7B9%7D)%7D)
3. Gunakan Uraian Deret
(http://latex.codecogs.com/gif.download?(1+%5Cfrac%7B2%7D%7B9%7D)%5E%7B0.5%7D=&space;1+0.5(%5Cfrac%7B2%7D%7B9%7D))
Nah, di poin yang ketiga ini yang saya kurang mengerti. Maksudnya uraian deret itu apa yah??
??? ???
4. Maka akar 11 = 3(1+ 1/9) = 3,333
Funsi (x) dapat diuraikan sebagai deret x^n atau dikenal sebagai deret Taylor atau deret sinus , cosinus yang dikenal sebagai deret Fourier, dst.
[pranala luar disembunyikan, sila masuk atau daftar.]
[pranala luar disembunyikan, sila masuk atau daftar.]
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Mtk Kerajaan Mataram pada September 01, 2010, 11:01:35 PM
Ditulis oleh: Mtk Kerajaan Mataram pada September 01, 2010, 11:01:35 PM
maka
Menurut deret Taylor
Mau mencari
Yang terdekat dibawah 11 yang bilangan kuadrat adalah 9, kita mengambil
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Sky pada September 08, 2010, 03:23:31 PM
Ditulis oleh: Sky pada September 08, 2010, 03:23:31 PM
Kutip dari: Nabih pada September 01, 2010, 09:14:23 AMLha, ini kan mintanya ngitung cepat.
Pake aja metode heron
Maksudnya pake metode Heron gimana?
Kutip dari: Fachni Rosyadi pada Agustus 12, 2010, 01:11:45 PMHaha... saya juga sering pake cara ini, karena untuk akar bilangan yang besar, jawabannya lumayan akurat.
Kalau caraku gini.
Misal kita ingin mencari nilai dari. Kita tahu bahwa
terletak antara
dan
.
Jadi,.
Soalnya, rentang pembagiannya makin lebar.
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Sky pada September 08, 2010, 03:34:35 PM
Ditulis oleh: Sky pada September 08, 2010, 03:34:35 PM
Sekadar memberitahu, ada juga cara estimasi lain, tapi saya lupa nama algoritmanya apa.
Mungkin yang lain tahu.
langkah-langkahnya seperti ini.
andaikan:

maka sudah pasti:

dan

Misal c=23
tentukan bilangan yang jika dikuadratkan kurang dari c, anggap bilangan ini a
misalkan a=4
apakah a x a = c?
Jika tidak, ambil b= c/a
tentukan a yang baru dengan cara:

Jika sudah didapat a, uji lagi apakah kuadrat dari a sama dengan c.
Jika tidak, ulangi terus langkah tadi.
Jika sudah, berarti a adalah akar c
Mungkin yang lain tahu.
langkah-langkahnya seperti ini.
andaikan:
maka sudah pasti:
dan
Misal c=23
tentukan bilangan yang jika dikuadratkan kurang dari c, anggap bilangan ini a
misalkan a=4
apakah a x a = c?
Jika tidak, ambil b= c/a
tentukan a yang baru dengan cara:
Jika sudah didapat a, uji lagi apakah kuadrat dari a sama dengan c.
Jika tidak, ulangi terus langkah tadi.
Jika sudah, berarti a adalah akar c
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Nabih pada September 18, 2010, 03:46:55 PM
Ditulis oleh: Nabih pada September 18, 2010, 03:46:55 PM
@Mtk Kerajaan Matram, Kreatif. But sepertinya kurang efektif
Judul: Re: Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: nandaz pada September 18, 2010, 07:59:51 PM
Ditulis oleh: nandaz pada September 18, 2010, 07:59:51 PM
guruku pernah mengajari cara ini untuk akar2 irrasional, tetapi ini aku tidak tau sumbernya dari mana, tetapi lumayan ampuh lho...cuma menggunakan kaidah kali, tambah, kurang aja :)

1x1 = 1 kemudian cari pengurangan bilangan dalam tanda akar dengan hasil kali tadi 3-1 =2, kali angka 2 dengan seratus (2x100 =200)
karena nominal awal 1, angka jumlah perkalian adalah dua. Cari dua digit berikut, (2Q x Q =200) yang mendekati nilai seratus Q=7 (maksudnya 27 x 7 = 189 dekat dengan 200) kita mendapati digit setelah 1 adalah 7, selanjutnya 200-189 = 11, 11 x 100 = 1100, lakukan cara yang sama (27 +7 = 34) kemudian (34Q x Q =1100) maka Q =3, karena 343 x 3 = 1029(angka2 yang mendekati hasil target) nah kita mendapati angka setelah digit 7 adalah 3...(kira2 hasilnya 1,73.....)nah silakan lanjutkan caranya
1x1 = 1 kemudian cari pengurangan bilangan dalam tanda akar dengan hasil kali tadi 3-1 =2, kali angka 2 dengan seratus (2x100 =200)
karena nominal awal 1, angka jumlah perkalian adalah dua. Cari dua digit berikut, (2Q x Q =200) yang mendekati nilai seratus Q=7 (maksudnya 27 x 7 = 189 dekat dengan 200) kita mendapati digit setelah 1 adalah 7, selanjutnya 200-189 = 11, 11 x 100 = 1100, lakukan cara yang sama (27 +7 = 34) kemudian (34Q x Q =1100) maka Q =3, karena 343 x 3 = 1029(angka2 yang mendekati hasil target) nah kita mendapati angka setelah digit 7 adalah 3...(kira2 hasilnya 1,73.....)nah silakan lanjutkan caranya
Judul: Re:Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Monox D. I-Fly pada Februari 01, 2014, 06:00:11 PM
Ditulis oleh: Monox D. I-Fly pada Februari 01, 2014, 06:00:11 PM
Kutip dari: Sky pada September 08, 2010, 03:34:35 PM
Sekadar memberitahu, ada juga cara estimasi lain, tapi saya lupa nama algoritmanya apa.
Mungkin yang lain tahu.
langkah-langkahnya seperti ini.
andaikan:
maka sudah pasti:
dan
Misal c=23
tentukan bilangan yang jika dikuadratkan kurang dari c, anggap bilangan ini a
misalkan a=4
apakah a x a = c?
Jika tidak, ambil b= c/a
tentukan a yang baru dengan cara:
Jika sudah didapat a, uji lagi apakah kuadrat dari a sama dengan c.
Jika tidak, ulangi terus langkah tadi.
Jika sudah, berarti a adalah akar c
Itu namanya Metode Bisection bukan?
Judul: Re:Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Sandy_dkk pada Februari 28, 2014, 12:38:22 PM
Ditulis oleh: Sandy_dkk pada Februari 28, 2014, 12:38:22 PM
dengan metode Babilonia.
dalam algoritma, menghitung nilai bilangan irasional sebenarnya adalah persoalan NP, namun bisa di-polynomial-kan dengan memberikan toleransi hasil perhitungan pada batasan tertentu.
bagaimana cara perhitungan dengan metode babilonia secara manual?
misalnya kita ingin mencari akar dari sebuah bilangan yaitu i, langkah pertama yang kita lakukan adalah mengestimasi sembarang bilangan sebagai hasil dari √i, misalnya √i = r .
nah, jika √i = r atau r2 = i , maka tentu akan memenuhi persamaan berikut:
( r + i/r ) / 2 = r .
dari mana rumus tsb diperoleh?
(r+r)/2 = r
r2 = i
( r + r2/r ) / 2 = r
( r + i/r ) / 2 = r .
sekarang, mari kita cari √2:
kita estimasi nilai r = 1 (anda bebas memilih estimasi nilai berapa saja).
maka: ( 1 + 2/1 ) / 2 = 1,5 <= 1,5-1=0,5 <= apakah anda puas dengan toleransi ini? jika belum,
maka: ( 1,5 + 2/1,5 ) / 2 = 1,41667 <= 1,5-1,41667=0,18333 <= apakah anda puas dengan toleransi ini? jika belum,
maka: ( 1,41667 + 2/1,41667 ) / 2 = 1,41422 <= 1,41667-1,41422=0,00245 <= apakah anda puas dengan toleransi ini? jika belum,
maka: ( 1,41422 + 2/1,41422 ) / 2 = 1,41421 <= 1,41422-1,41421=0,00001 <= apakah anda puas dengan toleransi ini? jika belum,
maka: ( 1,41421 + 2/1.41421 ) / 2 = 1,41421 <= 1,41421-1,41421=0,00000 <= jika anda sepakat dengan ketelitian lima angka di belakang koma yang saya gunakan, maka mestinya anda sudah puas dengan hasil ini!
sekarang, silahkan cari √3, √5, dll...
dalam algoritma, menghitung nilai bilangan irasional sebenarnya adalah persoalan NP, namun bisa di-polynomial-kan dengan memberikan toleransi hasil perhitungan pada batasan tertentu.
bagaimana cara perhitungan dengan metode babilonia secara manual?
misalnya kita ingin mencari akar dari sebuah bilangan yaitu i, langkah pertama yang kita lakukan adalah mengestimasi sembarang bilangan sebagai hasil dari √i, misalnya √i = r .
nah, jika √i = r atau r2 = i , maka tentu akan memenuhi persamaan berikut:
( r + i/r ) / 2 = r .
dari mana rumus tsb diperoleh?
(r+r)/2 = r
r2 = i
( r + r2/r ) / 2 = r
( r + i/r ) / 2 = r .
sekarang, mari kita cari √2:
kita estimasi nilai r = 1 (anda bebas memilih estimasi nilai berapa saja).
maka: ( 1 + 2/1 ) / 2 = 1,5 <= 1,5-1=0,5 <= apakah anda puas dengan toleransi ini? jika belum,
maka: ( 1,5 + 2/1,5 ) / 2 = 1,41667 <= 1,5-1,41667=0,18333 <= apakah anda puas dengan toleransi ini? jika belum,
maka: ( 1,41667 + 2/1,41667 ) / 2 = 1,41422 <= 1,41667-1,41422=0,00245 <= apakah anda puas dengan toleransi ini? jika belum,
maka: ( 1,41422 + 2/1,41422 ) / 2 = 1,41421 <= 1,41422-1,41421=0,00001 <= apakah anda puas dengan toleransi ini? jika belum,
maka: ( 1,41421 + 2/1.41421 ) / 2 = 1,41421 <= 1,41421-1,41421=0,00000 <= jika anda sepakat dengan ketelitian lima angka di belakang koma yang saya gunakan, maka mestinya anda sudah puas dengan hasil ini!
sekarang, silahkan cari √3, √5, dll...
Judul: Re:Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Sandy_dkk pada Februari 28, 2014, 12:43:40 PM
Ditulis oleh: Sandy_dkk pada Februari 28, 2014, 12:43:40 PM
kita bebas memilih nilai estimasi berapapun, bebas juga memilih tingkat ketelitian berapa angkapun di belakang koma. hanya saja, semakin estimasinya jauh dari nilai yang sebenarnya dan semakin tinggi ketelitian yang kita inginkan, maka perhitungannya akan semakin panjang...
Judul: Re:Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: blacknait pada Juni 16, 2014, 05:24:24 PM
Ditulis oleh: blacknait pada Juni 16, 2014, 05:24:24 PM
Pakai aproksimasi dari diferensial juga bisa bro
dy/dx = delta y / delta x
dy/dx = delta y / delta x
Judul: Re:Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Sandy_dkk pada Juni 19, 2014, 10:51:33 AM
Ditulis oleh: Sandy_dkk pada Juni 19, 2014, 10:51:33 AM
Kutip dari: blacknait pada Juni 16, 2014, 05:24:24 PM
Pakai aproksimasi dari diferensial juga bisa bro
dy/dx = delta y / delta x
bagaimana mencari √5 dengan metode ini? monggo contohnya kang...
Judul: Re:Memecahkan Akar Kuadrat Irrasional tanpa Kalkulator
Ditulis oleh: Monox D. I-Fly pada Mei 31, 2016, 09:29:37 AM
Ditulis oleh: Monox D. I-Fly pada Mei 31, 2016, 09:29:37 AM
Kutip dari: Nabih pada September 01, 2010, 09:14:23 AM
Pake aja metode heron
Heron... Rumus luas segitiga yang diketahui ketiga sisinya itu?