Forum Sains Indonesia

Hai Bro n Sis!

Dah lama nih gak ngulik-ngulik lagi topik tentang Matematik.

Btw.. Mau nanya aja sekarang!

Bagaimana cara membuktikan 1 + 1 = 2

Apakah kita hanya bisa menerimanya bulat-bulat? Tanpa tahu keabsahannya?
Ataukah aritmatik seperti itu hanya sekedar simbol belaka?

hai bro sis..!!

klw menurut Aq cari aja pake tangan..!!!

caranya : cari taw dengan jarimu...!!!

Hehehe....
kadang gw juga suka kepikiran gitu tuh....  ;D

Kutip dari: swaziland pada Maret 29, 2008, 06:13:00 PM
Hehehe....
kadang gw juga suka kepikiran gitu tuh....  ;D

Kutip dari: iann pada Maret 29, 2008, 05:39:30 PM
hai bro sis..!!

klw menurut Aq cari aja pake tangan..!!!

caranya : cari taw dengan jarimu...!!!

hehe...
pake apa y????

Pake calculator!!!! hoho...


-----------------------
Maap, cm bcanda....  :P

mwu--uh~

iya juga, ya...

emang pembuktiannya apa, sih??

Coba lihat ini deh :

(http://joewhitson.com/db3/00271/joewhitson.com/_download/proof.bmp.bmp)

Inilah katanya pembuktian 1+1=2
Tapi ada yang bisa menterjemahkan gak? Simbol2 apaan sih itu?

kyknya 1+1=2 itu dah kesepakatan deh..  dan bisa dibuktikan

sama kyk angka yg pertama kali itu adalah 1 (satu)

klo mau diubah-ubah yah bikin aja peraturan sendiri

klo dak mau nerima ya bikin peraturan sendiri juga

kenapa hal yang sudah ada dan sudah menjadi ketetapan harus dicari-cari kesalahan atau kelemahannya

bukan mencari hal baru yang supaya bisa dikenal orang lain dan menjadi ketetapan juga

kalo saya pernah tau pembuktian bahwa 1 = 2
; sisi kiri di faktorkan dan sisi kanan satu a dikeluarkan
; kedua sisi dibagi (a - a)
; sehingga
; maka
;
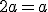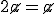; terbukti
2 = 1

;D

Kutip dari: musik_ajah pada April 28, 2008, 08:49:43 AM
kyknya 1+1=2 itu dah kesepakatan deh..  dan bisa dibuktikan

Nah.. pembuktiannya bagaimana?

Kutip dari: musik_ajah pada April 28, 2008, 08:49:43 AM
kenapa hal yang sudah ada dan sudah menjadi ketetapan harus dicari-cari kesalahan atau kelemahannya

bukan mencari hal baru yang supaya bisa dikenal orang lain dan menjadi ketetapan juga

Mungkin kalau Anda berkata hal tersebut di depan mr. Leonardo da Vinci, kuping Anda akan dijewernya! hehe...  ;D (*bercanda). Perhatikanlah perkataan seorang ilmuwan (yang sampai saat ini belum ada tandingannya) dalam memberikan sebuah pelajaran pertama kepada pengagum2nya, dan kepada mereka-mereka yang ingin berguru ilmu kepadanya :

Kutip“No human investigations can be called true science without going through mathematical tests”

Leonardo da Vinci (1452 â€" 1519), Italian Artist and Scientist

Jangan menerima kebenaran sesuatu bila :
1. Kita sendiri belum menemukan kebenarannya
2. Bila kita memang manusia yang tidak punya kekuatan untuk membuktikannya

Saya sebagai "pencinta matematik" sedang tergila-gila terhadap hal-hal yang remeh, yang bisa jadi membuat sebuah hal yang besar. Inget teori Butterfly effect kan? (atau teori Chaos), segala hal yang kecil tidak bisa kita anggap remeh, sebab suatu saat kelak bisa jadi memberikan dampak yang begitu besar. hehe... kok jadi kemana-mana yach...!!  ;D (maklum salah minum obat!)

Kutip dari: superstring39 pada Mei 08, 2008, 03:56:02 PM
kalo saya pernah tau pembuktian bahwa 1 = 2
; sisi kiri di faktorkan dan sisi kanan satu a dikeluarkan
; kedua sisi dibagi (a - a)
; sehingga
; maka
;
; terbukti
2 = 1

;D

Menarik juga nih..!
Hahaha..... eh.. kurang satu ha-nya.. (hahahaha......!)  :D
Hihi... coba aku patahkan pembuktian ini yach...!  ;D

Ambil pemisalan a = 1, maka :
; sisi kiri di faktorkan dan sisi kanan satu a dikeluarkan

Terus persamaan ini mau kita bagi dengan (a-a) alias (1-1) = 0
Gila aja...! Anda telah menulis sebuah persamaan yang membuat profesor se-genius apapun bisa STRESS bahkan komputer saja bisa CRASH! Kenapa? Karena angka NOL masih sebuah misteri yang tetap akan menjadi misteri. Angka yang "tidak ada" akan tetapi "harus ada". Angka yang benar-benar misterius. Saya pikir, dalam postingan sebelumnya sudah dibahas yach tentang angka nol ini, jadi tidak akan saya diulang!

Simplenya : Pembagian dengan NOL adalah TIDAK MUNGKIN. Hasilnya tidak terdefinisikan!

So penyelesaian yang ditulis :

Kutip dari: superstring39 pada Mei 08, 2008, 03:56:02 PM
; kedua sisi dibagi (a - a)
; sehingga
; maka
;

hanya sebuah canda matematik yang sangat menarik!

Menarik memang bicara matematika, kalau saya tidak melihat dulu profesionalitas dalam matematika. Hanya semoga bisa semakin berpikir rasional.
Kalo melihat melihat cara pembuktian shg diperoleh 2=1, memang tidak sah, karena membagi (mem-partisi) suatu bilangan tak nol dengan nol adalah tak mungkin. Kalo misalnya digunakan model pengertian limit, maka
untuk pangkat 2
Lim_x->a(x²-a²)/(x-a)
=Lim_x->a(x-a)(x+a)/(x-a)=2a
Lalu untuk pangkat 3
Lim_x->a(x³-a³)/(x-a)
=Lim_x->a(x-a)(x²+ax+a²)/(x-a)=3a²
Dan seterusnya misalnya untuk pangkat n,
Lim_x->a(xⁿ-aⁿ)/(x-a)
=Lim_x->a(x-a)(x^(n-1)+ax^(n-2)+...+a^(n-1))/(x-a)=na^(n-1)

Jadi kalo melihat dari sini, pembagian dengan nol diperbolehkan, maka tidak hanya akan menghasilkan 1=2, tapi bisa juga 1=3, 1=4, dst, tentu saja bukan merupakan definisi yang dapat disahkan.

Kalo bahasa keseharian memang bisa saja 0 dikatakan mewakili 'tidak ada'. Kalo kita misalnya melihat dalam pembahasan struktur aljabar, nol dikaitkan sebagai elemen identitas(netral) untuk operasi biner penjumlahan, dalam hal ini fungsinya sama dengan 1 (satu) untuk operasi biner perkalian.

Peace

 ;)sebenernya 1+1 itu hanya sebuah simbol yang mengartikan bahwa jika kita punya satu donat dan ketika kita membeli satu donat lagi kita akan mempunyai dua donat. dan dua itu adalah donat yang kita punya, jika sekarang kita mau mengubah angka dua itu dengan x,y, ataupun 3 pun tidak masalah yang penting kita tahu maksudnya ya sebanyak itu.

maaf klo postingan saya sebelumnya tidak memuaskan.. hehe maklum orang bodoh.. -_-"

Kutip dari: thhiinnkk pada Juni 06, 2008, 03:24:18 PM
;)sebenernya 1+1 itu hanya sebuah simbol yang mengartikan bahwa jika kita punya satu donat dan ketika kita membeli satu donat lagi kita akan mempunyai dua donat. dan dua itu adalah donat yang kita punya, jika sekarang kita mau mengubah angka dua itu dengan x,y, ataupun 3 pun tidak masalah yang penting kita tahu maksudnya ya sebanyak itu.

tapi saya setuju dengan tulisan ini..
hal yg simple dan sudah dipelajari di kelas 3 sd ini seharusnya memang tak usah dipersoalkan.. peace and love ahh

untuk membuktikan 1+1=2 diperlukan
1. pengertian mengenai himpunan bilangan cacah.
{0, 1, 2, ....}

2. urutan (suksesor dan predesesor) dalam bilangan-bilangan tersebut.
contoh: suksesor 0 adalah 1 dan seterusnya.

3. didefinisikan tanda a + 1 operasi suksesor setelah bilangan a
contoh: 5 + 1 adalah suksesor dari 1, yaitu 6.
sedangkan untuk 0 adalah bilangan netral.
begitu juga dengan tanda - (invers dari suksesor atau predesesor).

begitu yang masih aku inget dari kuliah Konsep Bilangan.
dari hal itu muncul teorema teorema berkaitan dengan jumlah penjumlahan
seperti
a + b = a + 1 + (b-1). teorema ini yang biasanya dipergunakan untuk membuktikan contoh-contoh seperti
4 + 3 = 4 + 1 + 2 = 4 + 1 + 1 + 1
yang artinya suksesor-suksesor-suksesor dari 4 adalah 7 (lihat himpunan bilangan cacah yang sudah definisikan sebelumnya)

nah, untuk 1 + 1 = 2, dengan definisi di atas saja sudah langsung kelihatan, karena suksesor 1 adalah 2.


CMIIW dah...
kalo salah mohon dikoreksi ya... maklum dah agak lupa... :D

Satu itu angka pertama
Tambah itu kenaikan levet tingkatan angka..

1 + 1
Artinya Angka pertama naik 1 tingkat

= 2
Berarti menghasilkan angka yang kedua

:D :D :D

Kalo 1+1=2 kenapa 2+0=2?

Kutip dari: reborn pada Juli 28, 2008, 04:13:20 PM
Kalo 1+1=2 kenapa 2+0=2?

Ini baru pertanyaan genius...apalagi yang katanya angka 0 merupakan angka misteri katanya tadi...kalau memang misteri kenapa bisa dipastikan 2 + 0 itu sama dengan 2???

Kutip dari: reborn pada Juli 28, 2008, 04:13:20 PM
Kalo 1+1=2 kenapa 2+0=2?

wakakakaka.... akhirnya pertanyaannya bertambah susah, walaupun dilihat secara kasat mata, cuman penjumlahan sederhana. Dan senada dengan perkataannya mozzpunkz, Nol merupakan misteri yang tetap akan jadi misteri. Jadi mengapa 2+0=2? Pembuktian matematisnya bagaimana? wah.. lieur.. lieur...!! orang genius memang suka nyari yang susah-susah.. hehehehe.... Nampaknya pendekatan logika (dua kue ditambah tidak bawa kue sama dengan dua kue) kurang memuaskan hasrat seorang reborn.  ;D

ayo.. silahkan...

Kutip dari: Vinchemz pada Juli 28, 2008, 04:10:45 PM
Satu itu angka pertama
Tambah itu kenaikan levet tingkatan angka..

1 + 1
Artinya Angka pertama naik 1 tingkat

= 2
Berarti menghasilkan angka yang kedua

:D :D :D

Karena setelah Satu itu angka Dua
Dan Tambah itu kenaikan level tingkatan angka..

2 + 0
Artinya Angka Kedua naik 0 tingkat

= 2
Berarti menghasilkan angka yang kedua (tidak berubah, sering disebut sifat identitas)

pertanyaan selanjutnya.
kenapa negatif dikali negatif bisa jadi positif

contoh:
(-2) x (-3) = 6

Halo.... salam kenal semuanya,
aku Alfian anak kelas 6 SD
pembuktianku

Dalam rumus matematika ada:



Kita pakai cara itu untuk membuktikan




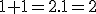
Terbukti

Kutip dari: musik_ajah pada Mei 27, 2009, 05:55:08 AM
pertanyaan selanjutnya.
kenapa negatif dikali negatif bisa jadi positif

contoh:
(-2) x (-3) = 6

Nah, kalau ini bisa dilihat disini http://www.forumsains.com/matematika/min-kali-min-plus/

Kutip dari: Alfian Rahman pada Juni 05, 2009, 05:15:24 AM
Halo.... salam kenal semuanya,
aku Alfian anak kelas 6 SD
pembuktianku

Dalam rumus matematika ada:



Kita pakai cara itu untuk membuktikan




Terbukti

Halo juga Alfian, salam kenal..
Nah, itulah yang dipertanyakan oleh Topic Starter, mengapa ditetapkan seperti itu.

Kalau buat saya, jawaban seperti ini sudah mencukupi untuk saya terima, (he.., soalnya bukan orang matematika)

Kutip dari: thhiinnkk pada Juni 06, 2008, 03:24:18 PM
sebenernya 1+1 itu hanya sebuah simbol yang mengartikan bahwa jika kita punya satu donat dan ketika kita membeli satu donat lagi kita akan mempunyai dua donat. dan dua itu adalah donat yang kita punya, jika sekarang kita mau mengubah angka dua itu dengan x,y, ataupun 3 pun tidak masalah yang penting kita tahu maksudnya ya sebanyak itu.

setuju ma idad itu hanya sebuah simbol

[pranala luar disembunyikan, sila masuk atau daftar.]

sapa bilang 1+1=2?
bisa kok satu tambah satu sama dengan 10. tapi kalo orang biologi yang jawab. satu ibu "ditambah" satu ayah kan bisa menghasilkan sepuluh. haha. (LOL bro)

salam kenal aja tuk semuanya
saia orang baru yang kesasar di forum ini

Kutip dari: musik_ajah pada Mei 27, 2009, 05:55:08 AM
pertanyaan selanjutnya.
kenapa negatif dikali negatif bisa jadi positif

contoh:
(-2) x (-3) = 6

slam knal bro,,,mf q orng bru pngen ikutn ne,,

q mo cba jwb ne yah :
mengapa di matematika min kali min = plus ( - * - =  +)
kayak  -1 x -1 = 1

sbgi alat tuk ngjlasn kt pakek yg ne :
1. jika a Anggota Bilangan Bulat, maka a + (-a) = 0, (sifat inpers pnjumlahn)
2. jika a Anggota Bilangan Bulat, maka a x 0 = 0 (sifat prkalian dgn 0 ))
3. jika a, b, c Anggota Bilangan Bulat, dan a + c = b + c, maka a = b
4. (a) . (-b) = - (a.b), (yg ni dah d bktiin seblm na)

trz kt cba pakek alat na tuk buktiin min kali min = plus atau kt msalkn dgn (-a) . (-b) = a.b

(-a) . [b + (-b) ]= (-a) . 0 = 0 (dari alat 1 dan 2)
(-a) . [b + (-b) ]= [(-a) . b] + [(-a) . (-b)]  (sifat distributif prkalian trhdp pnjmlahn ))

dgn sifat kesamaan, dua hal d atas dpt d artikn bhwa : [(-a) . b] + [(-a) . (-b)]  = 0
slanjt na dgn alat ' 4 ', ksmpuln tsb kt ubh mnjdi             : [- (a . b)] + [(-a) . (-b)]  = 0

kt ketahui bhwa [- (a . b)] + (a . b) = 0, (ats dasar alat "1"), mka prsmaan d atas dpt kt tulis :
[- (a . b)] + [(-a) . (-b)]  = [- (a . b)] + (a . b)

Nah...! dgn brdsar sma alat "3", kt peroleh : [(-a) . (-b)]  = (a . b)

Kutip dari: insan sains pada Maret 29, 2008, 12:25:20 PM
Hai Bro n Sis!

Dah lama nih gak ngulik-ngulik lagi topik tentang Matematik.

Btw.. Mau nanya aja sekarang!

Bagaimana cara membuktikan 1 + 1 = 2

Apakah kita hanya bisa menerimanya bulat-bulat? Tanpa tahu keabsahannya?
Ataukah aritmatik seperti itu hanya sekedar simbol belaka?

ribet jg yah,,, ;D

Kutip dari: superstring39 pada Mei 08, 2008, 03:56:02 PM
kalo saya pernah tau pembuktian bahwa 1 = 2
; sisi kiri di faktorkan dan sisi kanan satu a dikeluarkan
; kedua sisi dibagi (a - a)
; sehingga
; maka
;
; terbukti
2 = 1

;D

gilak,,

masa 0/0 dianggap satu, yang bener aja, pembodohan nih namanya, :(

1 + 1 tidak selalu sama dengan 2

1 + 1 = 1 kalau dalam aljabar bolean
1 + 1 = 10 kalau dalam biner

Kutip dari: reborn pada Juli 28, 2008, 04:13:20 PM
Kalo 1+1=2 kenapa 2+0=2?

Kalau 1 + 1 = 2 dan 1 - 1 = 0 bukannya pembuktian 2 + 0 = 2 itu mudah?

2 + 0 = 2
(1 + 1) + (1 - 1) = 1 + 1
1 + 1 + 1 - 1 = 1 + 1
1 + 1 = 1 + 1
Terbukti