Judul: Pembuktian Hal Dasar
Ditulis oleh: biobio pada April 23, 2009, 04:23:28 PM
Ditulis oleh: biobio pada April 23, 2009, 04:23:28 PM
Saya ingin nanya, bagaimana pembuktian matematis dari:
1. -1 x -1 = 1
2. -1 x a = -a
3. a (pangkat) 0 = 1
4. 1 + 1 = 2
5. 5/0=?
Apa ada beberapa dari pertanyaan yang saya ajukan tadi adalah sebuah aksioma matematika? Dan sebenarnya ada berapa sih aksioma matematika itu? Apa aja?
1. -1 x -1 = 1
2. -1 x a = -a
3. a (pangkat) 0 = 1
4. 1 + 1 = 2
5. 5/0=?
Apa ada beberapa dari pertanyaan yang saya ajukan tadi adalah sebuah aksioma matematika? Dan sebenarnya ada berapa sih aksioma matematika itu? Apa aja?
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Sky pada April 24, 2009, 10:20:50 AM
Ditulis oleh: Sky pada April 24, 2009, 10:20:50 AM
kayaknya aksioma deh.
Kalo dasar bukanlah aksioma, terus nanti gimannna caranya bikin teorema?
tapi kalo nomor 3 itu teorema kayaknya.
soalnya bukan hal dasar.
Kalo dasar bukanlah aksioma, terus nanti gimannna caranya bikin teorema?
tapi kalo nomor 3 itu teorema kayaknya.
soalnya bukan hal dasar.
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: biobio pada April 25, 2009, 04:50:08 PM
Ditulis oleh: biobio pada April 25, 2009, 04:50:08 PM
hmmm...no.3 udah mulai dapet ilham,misalkan 2^5 / 2^3, bisa ditulis sebagai 2^(5-3),maka 2^2 / 2^2 = 2^0, dan dihitung manual 2x2 / 2x2 = 1,maka 2^0 adalah 1, x^0=1,gitu?sah ga ya?
@sky:
apa definisi aksioma?
huaah...mana ni MTk Kerajaan Mataram yg jago mat itu?
@sky:
apa definisi aksioma?
huaah...mana ni MTk Kerajaan Mataram yg jago mat itu?
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Sky pada April 25, 2009, 05:32:55 PM
Ditulis oleh: Sky pada April 25, 2009, 05:32:55 PM
@biobio
Lha? kan tadi nanya itu aksioma atau bukan. Kirain udah tau definisi aksioma.
Ringkasnya, aksioma itu adalah dasar pembuktian.
Jadi, aksioma itu bukan untuk dibuktikan.
Untuk menguji aksioma itu benar atau tidak, bukan dengan cara mencari darimana
asal aksioma, tapi menggunakan aksioma untuk membuktikan teorema atau kebenaran umum.
Lebih lanjut lagi, aksioma itu bisa datang darimana saja. Kita tidak perlu mementingkan bagaimana hal itu bisa jadi aksioma, tapi dari calon aksioma itu, apakah bisa menjadi suatu kebenaran.
Sebenarnya postulat itu bisa disebut juga nama lain aksioma.
Contohnya postulat Einstein.
Einstein bilang hukum fisika berlaku sama di semua kerangka inersia.
Tapi pernyataan Einstein ini tidak berdasar atau istilahnya tiba-tiba muncul begitu saja tanpa penurunan.
Tapi, dari pernyataan ini, dia dapat merumuskan Teori Relativitas yang terbukti cocok dengan hasil eksperimen.
kira-kira seperti itu yang saya tahu
Lha? kan tadi nanya itu aksioma atau bukan. Kirain udah tau definisi aksioma.
Ringkasnya, aksioma itu adalah dasar pembuktian.
Jadi, aksioma itu bukan untuk dibuktikan.
Untuk menguji aksioma itu benar atau tidak, bukan dengan cara mencari darimana
asal aksioma, tapi menggunakan aksioma untuk membuktikan teorema atau kebenaran umum.
Lebih lanjut lagi, aksioma itu bisa datang darimana saja. Kita tidak perlu mementingkan bagaimana hal itu bisa jadi aksioma, tapi dari calon aksioma itu, apakah bisa menjadi suatu kebenaran.
Sebenarnya postulat itu bisa disebut juga nama lain aksioma.
Contohnya postulat Einstein.
Einstein bilang hukum fisika berlaku sama di semua kerangka inersia.
Tapi pernyataan Einstein ini tidak berdasar atau istilahnya tiba-tiba muncul begitu saja tanpa penurunan.
Tapi, dari pernyataan ini, dia dapat merumuskan Teori Relativitas yang terbukti cocok dengan hasil eksperimen.
kira-kira seperti itu yang saya tahu
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: biobio pada April 25, 2009, 05:34:27 PM
Ditulis oleh: biobio pada April 25, 2009, 05:34:27 PM
Kutip dari: Sky pada April 25, 2009, 05:32:55 PMsori...bukan definisi aksioma,tapi teorema..
@biobio
Lha? kan tadi nanya itu aksioma atau bukan. Kirain udah tau definisi aksioma.
Ringkasnya, aksioma itu adalah dasar pembuktian.
Jadi, aksioma itu bukan untuk dibuktikan.
Untuk menguji aksioma itu benar atau tidak, bukan dengan cara mencari darimana
asal aksioma, tapi menggunakan aksioma untuk membuktikan teorema atau kebenaran umum.
Lebih lanjut lagi, aksioma itu bisa datang darimana saja. Kita tidak perlu mementingkan bagaimana hal itu bisa jadi aksioma, tapi dari calon aksioma itu, apakah bisa menjadi suatu kebenaran.
Sebenarnya postulat itu bisa disebut juga nama lain aksioma.
Contohnya postulat Einstein.
Einstein bilang hukum fisika berlaku sama di semua kerangka inersia.
Tapi pernyataan Einstein ini tidak berdasar atau istilahnya tiba-tiba muncul begitu saja tanpa penurunan.
Tapi, dari pernyataan ini, dia dapat merumuskan Teori Relativitas yang terbukti cocok dengan hasil eksperimen.
kira-kira seperti itu yang saya tahu
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Sky pada April 25, 2009, 05:50:37 PM
Ditulis oleh: Sky pada April 25, 2009, 05:50:37 PM
kalo Teorema itu pernyataan yang sudah dibuktikan dengan menggunakan aksioma atau teorema yang lain.
Kenapa perlu ada teorema dan perlu dibuktikan?
Karena Teorema itu akan digunakan untuk membuktikan teorema yang lain, dan teorema dapat memudahkan menyelesaikan problem ilmiah. sekaligus dapat dengan aman dipakai karena sudah teruji kebenarannya.
Kenapa perlu ada teorema dan perlu dibuktikan?
Karena Teorema itu akan digunakan untuk membuktikan teorema yang lain, dan teorema dapat memudahkan menyelesaikan problem ilmiah. sekaligus dapat dengan aman dipakai karena sudah teruji kebenarannya.
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Mtk Kerajaan Mataram pada April 26, 2009, 05:31:26 PM
Ditulis oleh: Mtk Kerajaan Mataram pada April 26, 2009, 05:31:26 PM
Kutip dari: biobio pada April 23, 2009, 04:23:28 PMAksioma :
Saya ingin nanya, bagaimana pembuktian matematis dari:
1. -1 x -1 = 1
2. -1 x a = -a
* Jika dua bilangan real a dan b dijumlahkan hasilnya 0, maka a = -b
* -(-a) = a untuk semua bilangan real.
* a x b = b x a, perkalian bilangan real bersifat komutatif.
(-1) x a = a x (-1) = -a
Karena (-1) x (-1) + (-1) x 1 = -1 x (-1 + 1) = -1 x 0 = 0
yang artinya (-1) x (-1) dan (-1) x 1 dijumlahkan nol, maka (-1) x (-1) =-((-1) x 1) = -(-1)=1
Kutip dari: biobio pada April 23, 2009, 04:23:28 PM
5. 5/0=?
Apa ada beberapa dari pertanyaan yang saya ajukan tadi adalah sebuah aksioma matematika? Dan sebenarnya ada berapa sih aksioma matematika itu? Apa aja?
Membagi dengan nol berarti membagi dengan 'tidak ada', artinya sebenarnya tidak membagi.
Anda saya minta mengiris ongol-ongol masing-masing sebesar tidak ada, maka otomatis ongol-ongolnya tidak teriris (terbagi).
Axiom : a statement or proposition that needs no proof because its truth is obvious, or one that is accepted as true without proof.
Theorem : a proposition that is not self-evident but that can be proved from accepted premises and so is established as a law or principle
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: insan sains pada April 27, 2009, 12:45:32 PM
Ditulis oleh: insan sains pada April 27, 2009, 12:45:32 PM
Heu heu.. mantabs...
Kalo jago-jago Math udah turun, kayaknya ada pencerahan... ;D
Topik ini masih belum selesai kan, soalnya masih ada pertanyaan yang tersisa.
@Mtk Kerajaan Mataram :
btw.. Ongol-ongol itu apaan sie? ;D
Kalo jago-jago Math udah turun, kayaknya ada pencerahan... ;D
Topik ini masih belum selesai kan, soalnya masih ada pertanyaan yang tersisa.
Kutip dari: biobio pada April 23, 2009, 04:23:28 PM
Dan sebenarnya ada berapa sih aksioma matematika itu? Apa aja?
@Mtk Kerajaan Mataram :
btw.. Ongol-ongol itu apaan sie? ;D
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: biobio pada April 27, 2009, 04:35:16 PM
Ditulis oleh: biobio pada April 27, 2009, 04:35:16 PM
Wah, mantap bro Mtk Kerajaan Mataram...tul, apa aja aksioma itu?
dan lebih mantap lagi kalau dijelasin apa arti ongol2...
dan lebih mantap lagi kalau dijelasin apa arti ongol2...
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Sky pada April 28, 2009, 07:29:53 PM
Ditulis oleh: Sky pada April 28, 2009, 07:29:53 PM
harta langka kayak mas mataram ga boleh disia-siakan.
Eh, iya, kalo dari kalimatnya, onggol-onggol itu kue bolu kali,ya?
Eh, iya, kalo dari kalimatnya, onggol-onggol itu kue bolu kali,ya?
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: insan sains pada April 29, 2009, 04:48:33 PM
Ditulis oleh: insan sains pada April 29, 2009, 04:48:33 PM
[OOT ya...]
Ternyata saya lebih penasaran sama istilah "ongol-ongol".
Setelah minta bantuan mbah Google, baru tahu deh apa itu ongol-ongol.
Ternyata kue mirip "cenil". Liat deh pictnya :
(http://k43.pbase.com/g4/76/410576/3/63199895.3a435sTU.jpg)
Yuk.. silahkan dimakan. Terus kita lanjutin lagi diskusinya...
Apa aja aksioma yang ada? ;D
Ternyata saya lebih penasaran sama istilah "ongol-ongol".
Setelah minta bantuan mbah Google, baru tahu deh apa itu ongol-ongol.
Ternyata kue mirip "cenil". Liat deh pictnya :
(http://k43.pbase.com/g4/76/410576/3/63199895.3a435sTU.jpg)
Yuk.. silahkan dimakan. Terus kita lanjutin lagi diskusinya...
Apa aja aksioma yang ada? ;D
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: HyawehHoshikawa pada April 29, 2009, 06:53:37 PM
Ditulis oleh: HyawehHoshikawa pada April 29, 2009, 06:53:37 PM
apa aja aksioma yang ad kayaknya ga usah dibahas deh,
misal:
aksioma 1:
1+1=2
aksioma 2:
1+2=3
....
ngga ada abisnya dong???
yang penting itu kan aksioma itu yang udah ga perlu pembuktian:
misalnya kayak dari 2 titik bisa dibuat 1 garis lurus,dari 2 garis yang tidak sejajar bisa diambil satu titik perpotongan,...
tapi kalo' dari 3 titik bisa dibikin fungsi kuadrat, itu aksioma ato teorema yah???
misal:
aksioma 1:
1+1=2
aksioma 2:
1+2=3
....
ngga ada abisnya dong???
yang penting itu kan aksioma itu yang udah ga perlu pembuktian:
misalnya kayak dari 2 titik bisa dibuat 1 garis lurus,dari 2 garis yang tidak sejajar bisa diambil satu titik perpotongan,...
tapi kalo' dari 3 titik bisa dibikin fungsi kuadrat, itu aksioma ato teorema yah???
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: utusan langit pada April 29, 2009, 07:13:25 PM
Ditulis oleh: utusan langit pada April 29, 2009, 07:13:25 PM
gimana cara membuktikan bahwa cos 120* = -1/2...............
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: ksatriabajuhitam pada April 29, 2009, 08:02:37 PM
Ditulis oleh: ksatriabajuhitam pada April 29, 2009, 08:02:37 PM
Kutip dari: utusan langit pada April 29, 2009, 07:13:25 PMdigambar aja :D (kalo 120o berarti x nya di sumbu negatif)
gimana cara membuktikan bahwa cos 120* = -1/2...............
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: utusan langit pada April 29, 2009, 08:39:33 PM
Ditulis oleh: utusan langit pada April 29, 2009, 08:39:33 PM
nol pangkat nol berapa?
bagaimana membuktikannya?
bagaimana membuktikannya?
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: HyawehHoshikawa pada April 30, 2009, 01:42:11 AM
Ditulis oleh: HyawehHoshikawa pada April 30, 2009, 01:42:11 AM
nol pangkat nol bukannya tidak terdefinisi yah?
soalnya aksiomanya kan:

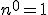
hmm...iya ga, ya... ???
soalnya aksiomanya kan:
hmm...iya ga, ya... ???
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: nash pada April 30, 2009, 06:53:40 AM
Ditulis oleh: nash pada April 30, 2009, 06:53:40 AM
@mtk kerajaan mataram
mav, aku mo balik lg nanya ttg aksioma, gapapa kan?
gini kak, jka kbenaran suatu aksioma dianggap mutlak tanpa pmbuktian, gmana caranya kita tau klo aksioma yg djadikan dasar teorema itu BENAR atau SALAH?
mav, aku mo balik lg nanya ttg aksioma, gapapa kan?
gini kak, jka kbenaran suatu aksioma dianggap mutlak tanpa pmbuktian, gmana caranya kita tau klo aksioma yg djadikan dasar teorema itu BENAR atau SALAH?
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Sky pada Mei 01, 2009, 09:55:13 AM
Ditulis oleh: Sky pada Mei 01, 2009, 09:55:13 AM
@nash
Eh,, maaf yang jawab malah saya...
Biar mas Mataram jawab yang bagian susahnya aja, haha...
nol pangkat nol memang tidak terdefinisi,kan?
bener ga sih?
Kalo di konsep limit, nol pangkat nol itu bentuk tak tentu.
Kutip dari: Sky pada April 25, 2009, 05:32:55 PMMaksudnya kalo Teorema yang dihasilkan dari aksioma tersebut itu benar (sesuai dengan eksperimen), maka aksioma itu mungkin benar .
Ringkasnya, aksioma itu adalah dasar pembuktian.
Jadi, aksioma itu bukan untuk dibuktikan.
Untuk menguji aksioma itu benar atau tidak, bukan dengan cara mencari darimana
asal aksioma, tapi menggunakan aksioma untuk membuktikan teorema atau kebenaran umum.
Eh,, maaf yang jawab malah saya...
Biar mas Mataram jawab yang bagian susahnya aja, haha...
nol pangkat nol memang tidak terdefinisi,kan?
bener ga sih?
Kalo di konsep limit, nol pangkat nol itu bentuk tak tentu.
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: biobio pada Mei 02, 2009, 07:56:26 PM
Ditulis oleh: biobio pada Mei 02, 2009, 07:56:26 PM
Kutip dari: utusan langit pada April 29, 2009, 08:39:33 PMgmana kalo pake cara bodoh2an syaa ini...
nol pangkat nol berapa?
bagaimana membuktikannya?
1. Kalo x^a dibagi x^b, hasilnya kan x^(a-b)
2. Maka kita coba 2^2 dibagi 2^2 juga... Hasilnya = 2^0
3. Persamaan kedua kita hitung manual... 2x2 / 2x2 = 1
4. Maka 2^0 = 1
5. Gimana, UL?
hahaha
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: utusan langit pada Mei 02, 2009, 08:03:25 PM
Ditulis oleh: utusan langit pada Mei 02, 2009, 08:03:25 PM
@ biobio
kayaknya nggak nyambung deh untuk kasus 0 pangkat 0,
0 pangkat 0 kan bisa saya artikan 0/0,
dengan a berapapun untuk model a/0, maka akan didapatkan hasil tak tentu!
hehehe ;D ;D ;D93x
kayaknya nggak nyambung deh untuk kasus 0 pangkat 0,
0 pangkat 0 kan bisa saya artikan 0/0,
dengan a berapapun untuk model a/0, maka akan didapatkan hasil tak tentu!
hehehe ;D ;D ;D93x
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: biobio pada Mei 02, 2009, 08:05:16 PM
Ditulis oleh: biobio pada Mei 02, 2009, 08:05:16 PM
wah, sory,..salah baca..gue pikir bilangan pangkat nol...hahaha
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: nash pada Mei 03, 2009, 06:52:25 AM
Ditulis oleh: nash pada Mei 03, 2009, 06:52:25 AM
0^0
= 0^2 / 0^2
= 0 / 0
= tak terdefinisi
gw rasa teorema
a^0 = 1
hanya brlaku jika a tdk sama dgn 0
= 0^2 / 0^2
= 0 / 0
= tak terdefinisi
gw rasa teorema
a^0 = 1
hanya brlaku jika a tdk sama dgn 0
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: utusan langit pada Mei 03, 2009, 07:00:59 AM
Ditulis oleh: utusan langit pada Mei 03, 2009, 07:00:59 AM
menganai konstanta phi, pada luas lingkaran (22/7)
darimana asal konstanta tersebut?
darimana asal konstanta tersebut?
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Sky pada Mei 03, 2009, 10:13:59 AM
Ditulis oleh: Sky pada Mei 03, 2009, 10:13:59 AM
maksudnya pi kali.
coba dicek di LaTex.
Tadinya matematikawan menemukan bahwa luas lingkaran sebanding dengan kuadrat jejari.
Lalu diberikan konstanta untuk membuat kesebandingan tadi jadi rumus.
jadilah L = pi r^2
coba dicek di LaTex.
Tadinya matematikawan menemukan bahwa luas lingkaran sebanding dengan kuadrat jejari.
Lalu diberikan konstanta untuk membuat kesebandingan tadi jadi rumus.
jadilah L = pi r^2
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: utusan langit pada Mei 03, 2009, 11:21:18 AM
Ditulis oleh: utusan langit pada Mei 03, 2009, 11:21:18 AM
KutipTadinya matematikawan menemukan bahwa luas lingkaran sebanding dengan kuadrat jejari.
Lalu diberikan konstanta untuk membuat kesebandingan tadi jadi rumus.
sebelum diketahui pi, gimana cara nentuin luasnya? ??? ??? ???
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: HyawehHoshikawa pada Mei 03, 2009, 02:58:36 PM
Ditulis oleh: HyawehHoshikawa pada Mei 03, 2009, 02:58:36 PM
D=diameter
tu yang dikuadratin 8d/9 nya yagh
lagian pi itu kan konstanta perbandingan antara keliling lingkaran dengan diameternya...
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Sky pada Mei 03, 2009, 03:08:47 PM
Ditulis oleh: Sky pada Mei 03, 2009, 03:08:47 PM
Kutip dari: utusan langit pada Mei 03, 2009, 11:21:18 AMBisa dengan cara yang sederhana ko.
sebelum diketahui pi, gimana cara nentuin luasnya? ??? ??? ???
Aku ga tau ini dipake ilmuwan jaman dulu atau engga.
Tapi, kalo saya:
Saya isi tabung lingkaran berjari-jari r, dan tinggi l dengan air (l bisa berapa aja, misalnya 1 satuan, biar gampang).
Selanjutnya, air saya pindahkan ke balok dengan alas yang sudah diketahui ( misalnya 1 satuan^2, biar gampang).
Lalu, tinggi airnya saya ukur.
Maka dapatlah Volume.
Lalu luas lingkaran didapat dengan cara mem bagi Volum dengan l.
Dapatlah luas lingkaran.
setelah mendapat banyak data jejari dan luas.
ya, dicari hubungannya....
dapat pi. (tapi nilainya masih kasar).
@hoshikawa
itu maksudnya rumus apa?
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: HyawehHoshikawa pada Mei 03, 2009, 03:26:04 PM
Ditulis oleh: HyawehHoshikawa pada Mei 03, 2009, 03:26:04 PM
ya rumus luas lingkaran dong...
orang yang ditanyain luas lingkaran
tapi itu diambil dari orang-orang arab...
misal yah

D = 2R
=>
=>
berapa itu 256/81?
monggo...ehe,namanya juga itungan orang jaman dulu
orang yang ditanyain luas lingkaran
tapi itu diambil dari orang-orang arab...
misal yah
D = 2R
=>
=>
berapa itu 256/81?
monggo...ehe,namanya juga itungan orang jaman dulu
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: HyawehHoshikawa pada Mei 05, 2009, 07:43:29 PM
Ditulis oleh: HyawehHoshikawa pada Mei 05, 2009, 07:43:29 PM
n^(1/x) = (1/n)^x
0^(n-n) = 0^n * (1/0)^n
0^(n-n) = 0^n * (1/0)^n
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Nabih pada Mei 24, 2009, 07:07:22 PM
Ditulis oleh: Nabih pada Mei 24, 2009, 07:07:22 PM
Kutip dari: HyawehHoshikawa pada April 29, 2009, 06:53:37 PM
tapi kalo' dari 3 titik bisa dibikin fungsi kuadrat, itu aksioma ato teorema yah???
Kayaknya teorema dech
Aksiomanya:
1. Axioma 1 Euclid (buku Elements)
2. Kalau ada 3 titik, belum tentu kolinear
3. Jika ada 3 titik yang tidak kolinear, maka ada 1 bidang yang melalui ketiganya
Setidaknya ada 3 aksioma yang mendasari hal tersebut ???
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: nash pada September 21, 2009, 10:46:28 AM
Ditulis oleh: nash pada September 21, 2009, 10:46:28 AM
Kutip dari: Mtk Kerajaan Mataram pada April 26, 2009, 05:31:26 PM
* -(-a) = a untuk semua bilangan real.
ini aksioma kah? tp kemarin ketemu soal utk membuktikan -(-a)=a
nah lho, berarti pernyataan tsb bukanlah aksioma :P
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: nash pada September 21, 2009, 10:47:03 AM
Ditulis oleh: nash pada September 21, 2009, 10:47:03 AM
Kutip dari: Mtk Kerajaan Mataram pada April 26, 2009, 05:31:26 PM
* -(-a) = a untuk semua bilangan real.
ini aksioma kah? tp kemarin ketemu soal utk membuktikan -(-a)=a
nah lho, berarti pernyataan tsb bukanlah aksioma :P
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: The Houw Liong pada September 21, 2009, 04:04:26 PM
Ditulis oleh: The Houw Liong pada September 21, 2009, 04:04:26 PM
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: HyawehHoshikawa pada September 21, 2009, 04:54:31 PM
Ditulis oleh: HyawehHoshikawa pada September 21, 2009, 04:54:31 PM
haah???
Integer???
bukan real yah?
eh, iya btw itu simbolnya om the houw liong, integral yang ada lingkaran ditengahnya tu artinya gimana ya?
pernah liat dibuku fisika...
Integer???
bukan real yah?
eh, iya btw itu simbolnya om the houw liong, integral yang ada lingkaran ditengahnya tu artinya gimana ya?
pernah liat dibuku fisika...
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: The Houw Liong pada September 21, 2009, 05:18:28 PM
Ditulis oleh: The Houw Liong pada September 21, 2009, 05:18:28 PM
-(-a)=a berlaku untuk integer, tetapi tentu bisa diperluas sehingga berlaku juga untuk bilangan real.
Di bawah jawaban mengenai pembuktian dasar integer tsb hanya latihan menulis dengan memakai mathtex saja
Judul: Re: Pembuktian Hal Dasar
Ditulis oleh: Mtk Kerajaan Mataram pada September 30, 2009, 07:49:07 AM
Ditulis oleh: Mtk Kerajaan Mataram pada September 30, 2009, 07:49:07 AM
Baik sifat berikut
Keduanya kalau diverbalkan menjadi "bilangan mempunyai invers".
Kalau pernah belajar mengenai struktur2 aljabar yang menghubungkan operasi biner dengan himpunan, maka tentu yakin bahwa ini merupakan aksioma bukan teorema.
Setiap 'group' bersifat bahwa setiap anggotanya punya invers, setiap 'ring' juga setiap anggotanya punya invers penjumlahan, setiap 'field' untuk setap anggotanya punya sekaligus invers penjumlahan dan perkalian....dst
Kutip dari: The Houw Liong pada September 21, 2009, 04:04:26 PMuntuk penjumlahan atau
a+(-a) = 0 atau a = -(-a)
Kutip dari: The Houw Liong pada September 21, 2009, 05:18:28 PMuntuk perkalian.
-(-a)=a
Keduanya kalau diverbalkan menjadi "bilangan mempunyai invers".
Kalau pernah belajar mengenai struktur2 aljabar yang menghubungkan operasi biner dengan himpunan, maka tentu yakin bahwa ini merupakan aksioma bukan teorema.
Setiap 'group' bersifat bahwa setiap anggotanya punya invers, setiap 'ring' juga setiap anggotanya punya invers penjumlahan, setiap 'field' untuk setap anggotanya punya sekaligus invers penjumlahan dan perkalian....dst
Judul: Re:Pembuktian Hal Dasar
Ditulis oleh: Monox D. I-Fly pada November 14, 2015, 09:45:15 AM
Ditulis oleh: Monox D. I-Fly pada November 14, 2015, 09:45:15 AM
Kutip dari: utusan langit pada April 29, 2009, 07:13:25 PM
gimana cara membuktikan bahwa cos 120* = -1/2...............
cos 120*
= cos (2 x 60)*
= cos260* - sin260*
= (½)2 - (½√3)2
= 1/4 - 3/4
= -1/2
Udah kan? :kribo: